Was könnte dieses Forum noch gebrauchen? Eine Anlaufstelle für interessante oder lustige Statistiken und Grafiken. Das können irgendwelche sein, die ihr irgendwo findet und natürlich mit Quellenangabe hier teilt oder auch gerne selbst erstellte.
Egal ob es eine aktuelle passing map eines Spiels von diesem Wochenende ist, oder sich jemand den Verlauf der Top 5 europäischen Frauen Ligen der letzten 20 Jahre angeschaut hat. Solange es interessant oder lustig ist, alles gern hier rein.
Die unten aufgeführte Tabelle soll eine schnelle Übersicht über nützliche Statistik-Seiten liefern. Eine ausführlichere und kommentierte Auflistung möglicher Quellen hat @Gnetzer in diesem Thread beschrieben.
Dieser Post ist als Wiki erstellt worden, so das alle die Tabellen ergänzen, korrigieren oder auf den neusten Stand bringen können.
| Webseite | Level | Live-Update? | Kommentar |
|---|---|---|---|
| understat.com | Einsteiger | nein | gute xG Grafiken |
| fotmob.com | Fortgeschritten 1 | ja | klicki-bunti aber nett aufbereitet |
| whoscored.com | Fortgeschritten 2 | ja | keine xG aber nützlicher Time-Slider |
| FBref.com | Hardcore Nerd | nein | unfassbar viele Daten und Export-Funktion! |
Auf Anfrage hier eine csv-Datei mit allen (Halbzeit-)Ergebnissen der Bundesliga seit ihrer Gründung. Ich werde versuchen die Datei halbwegs auf neustem Stand zu halten.
Letztes Update: Nach dem 15. Spieltag, Saison 2022/23
BuLiMatches.zip (111,9 KB)
Dann mache ich mal den Anfang. @bizzmane hatte vor einiger Zeit vorgeschlagen mal zu schauen, wie sich die Tabelle im Laufe einer Saison entwickelt, vor allem im Vergleich mit der Endtabelle. Während dieser „kurzen Auswertung“, tat sich aber ein kleiner Kaninchenbau auf und ich Trottel habe natürlich die rote Pille gewählt… Ich bitte hier schon einmal um Entschuldigung, dass es so lang geworden ist.
Kurze Warnung: Am Anfang wird es etwas trocken und technisch, dann wird es nerdy aber am Ende dann hoffentlich auch interessant. Außerdem noch der übliche Disclaimer: Das hier ist das Rasenfunkforum und kein Peer Review Journal, von daher das Folgende bitte nicht als die reine und unumstößliche Wahrheit sehen.
Wie wird gemessen?
Wenn wir zwei Tabellen miteinander vergleichen, gibt es intuitiv zwei Möglichkeiten dies zu tun:
Vergleiche für jedes Team die Positionen in beiden Tabellen und addiere die Differenz über alle Teams auf. Hier geht es also nur um die Position der Teams in den Tabellen, daher werde ich im Folgenden den Ausdruck „Position“ verwenden, wenn ich diese Zählweise meine.
Vergleiche für jede mögliche Paarung zweier Teams, ob Team A besser oder schlechter ist als Team B. Wenn dieser Vergleich in den beiden Tabellen unterschiedliche Ergebnisse gibt, gibt es einen Strafpunkt und am Ende werden alle Punkte aufsummiert. Hier geht es also nur um den relativen Vergleich zwischen den Teams, daher werde ich im Folgenden den Ausdruck „Relativ“ verwenden, wenn ich diese Zählweise meine.
Da ich nicht sagen kann welche Zählweise die Bessere ist, verwende ich einfach beide. Das hat auch den Vorteil um sicherzustellen, dass die Ergebnisse nicht durch die Zählweise beeinträchtigt werden. Für eine bessere Vergleichbarkeit, müssen die beiden Zählweisen renormiert werden: Dafür habe ich eine Tabelle genommen und eine Millionen mal die Reihenfolge zufällig auswürfeln lassen. Die randomisierten Tabellen wurden dann mittels beiden Zählweisen mit der Ausgangstabelle verglichen und resultierten beide Male in einer schönen gaußschen Glockenkurve – jeweils zentriert um 108 Punkte (Position) und 76,5 Punkte (Relativ). Daher werden diese beiden Werte jeweils als „100% Unordnung“ definiert. Werte kleiner als 100% heißen dementsprechend, dass es bereits eine gewisse Ordnung gibt und bei 0% sind die Tabellen identisch. Theoretisch wären im Einzelfall auch Werte von über 100% möglich, das wäre aber ein Indiz für Ordnung in entgegengesetzter Richtung und daher unwahrscheinlich. Bei ausreichend großen Stichproben sollte dies aber nicht auftreten – und wird hier auch nicht auftreten.
tl;dr: Zwei unterschiedliche Zählweisen, wobei beide so skaliert werden, dass ein Wert von 100 „absolutes Chaos“ bedeutet während ein „perfect match“ in einem Wert von 0 resultiert.
Saisons der letzten 30 Jahre:
Für die Auswertung, habe ich mir die Saisonverläufe 1992/93 bis 2021/22 angeschaut und durchgehend die Drei-Punkte-Regel angewandt. Nach jedem Spieltag wurde die Spieltagstabelle mit der Endtabelle verglichen und die Unordnung notiert.
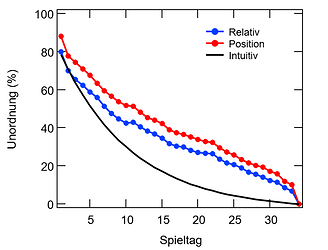
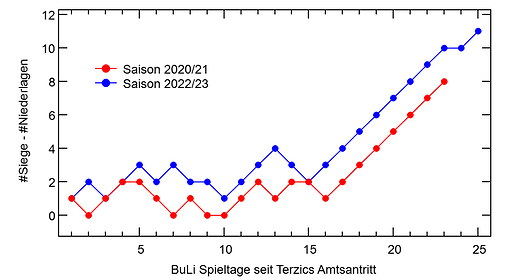
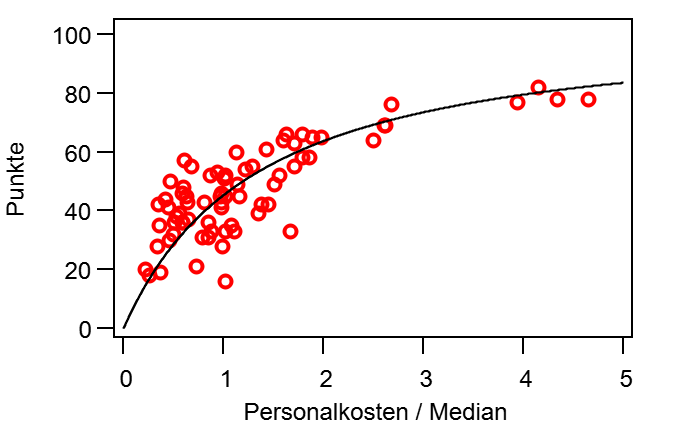
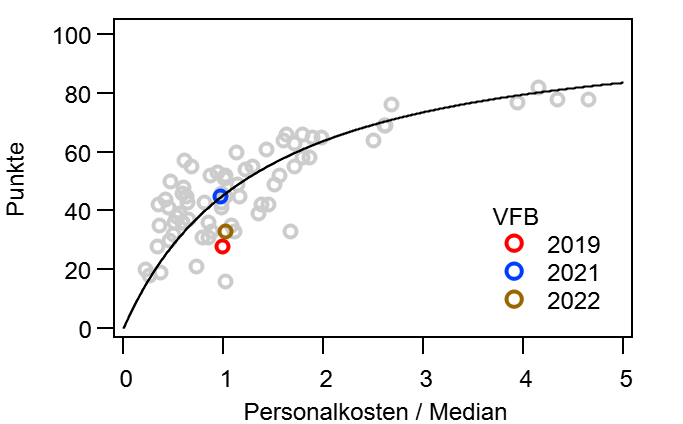
Der gemittelte Verlauf aller 30 Spielzeiten ist in Abbildung 1 für beide Zählweisen dargestellt und in beiden Fällen ist er in etwa linear. Dies hat mich überrascht, da ich intuitiv einen Verlauf erwartet hatte, der zumindest etwas asymptotisch ist (vgl schwarze Linie).
Abbildung 1
Hier tat sich dann auch der Kaninchenbau auf. Was macht man nämlich, wenn man einen komplexen Sachverhalt nicht versteht? Man baut sich ein eigenes Modell und spielt damit rum!
Ich bau’ mir ein Schloss aus Sand Modell
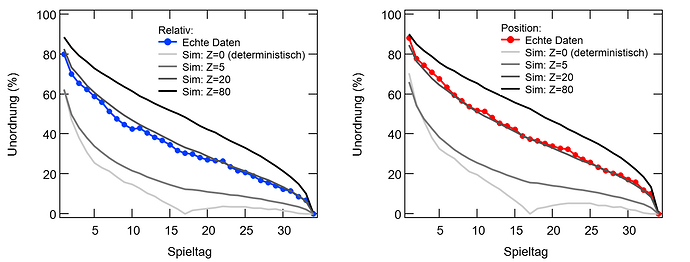
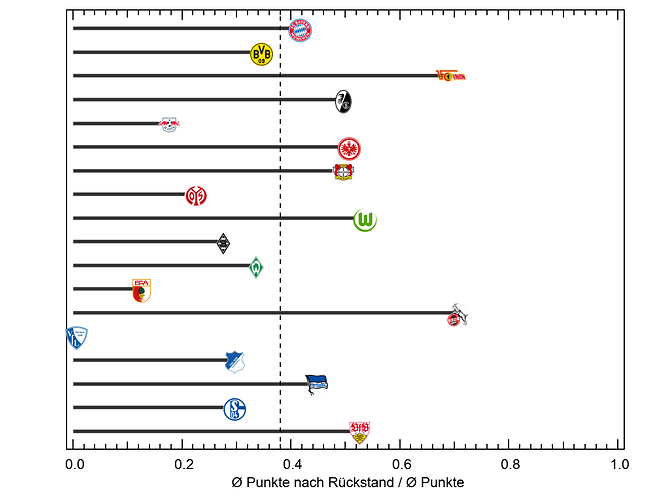
Um die Saisonverläufe zu simulieren, habe ich die gleichen Spielpläne verwendet und vorher für die 18 generischen Teams ein Power Ranking erstellt. Wenn nun zwei Teams gegeneinander spielen, ist der Ausgang abhängig von der Differenz ihrer Positionen im Power Ranking. Dafür habe ich mich an dem ELO Modell im Schach bedient und etwas abgewandelt, aber ich will euch an dieser Stelle nicht mit den Details langweilen. Wichtig ist nur: Es gibt einen Parameter Z mit dem man den Einfluss des Zufalls dosieren kann. Bei Z=0 gibt es keinen Zufall und das bessere Team gewinnt immer. Dieser Fall ist dargestellt in Abbildung 2 als hellste graue Linie. Wenn immer das bessere Team gewinnt, gibt es einen etwas asymptotischen Verlauf bis zum 17ten Spieltag, da hier jedes Team einmal gegen jedes andere gespielt hat. Mit Beginn der Rückrunde bricht diese Ordnung wieder auf, da der Spielplan wieder etwas Unordnung rein bringt, bis es zum Ende der Saison wieder perfekt sortiert ist.
Abbildung 2
Die dunkelgrauen Linien in Abbildung 2 entsprechen Saisonverläufe für verschiedene Werte für Z. Wie man erkennen kann, wird der Saisonverlauf relativ gut reproduziert für einen Wert von Z=20. Dies entspricht einer Sieg-Unentschieden-Niederlage Wahrscheinlichkeit von 35% : 33% : 32% bei einem Platz unterschied im Power Ranking und 51% : 31% : 18% bei 10 Plätzen Differenz.
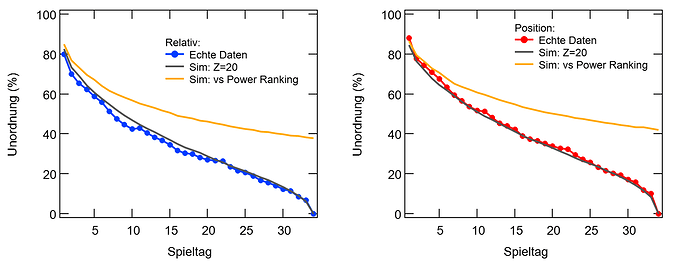
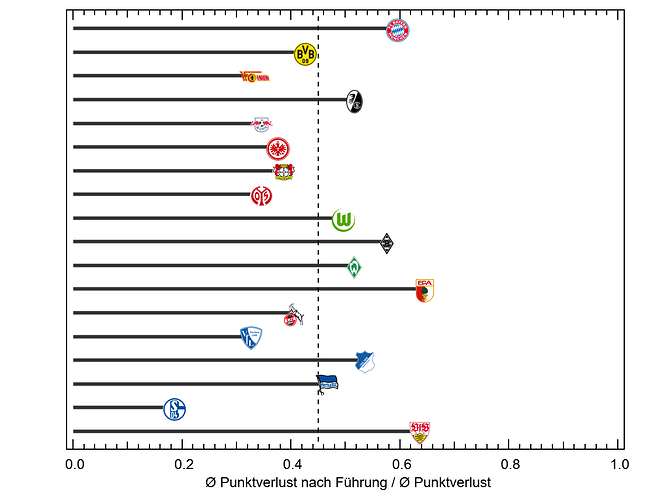
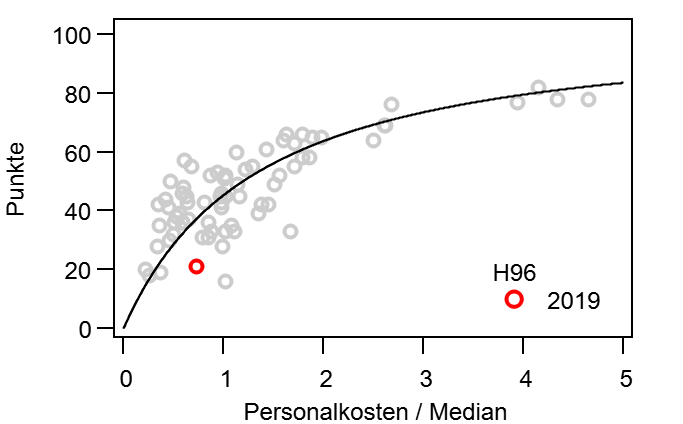
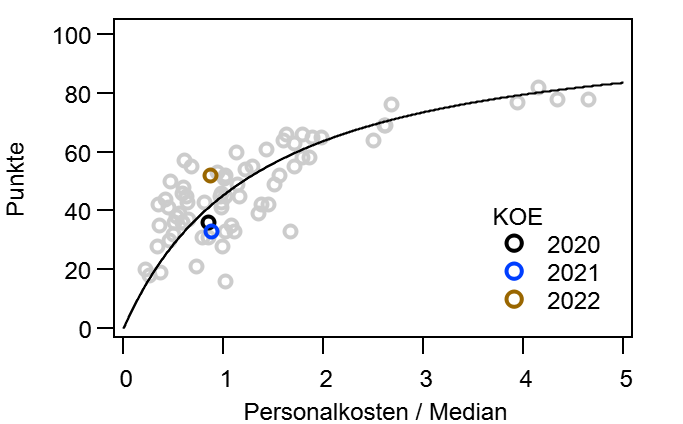
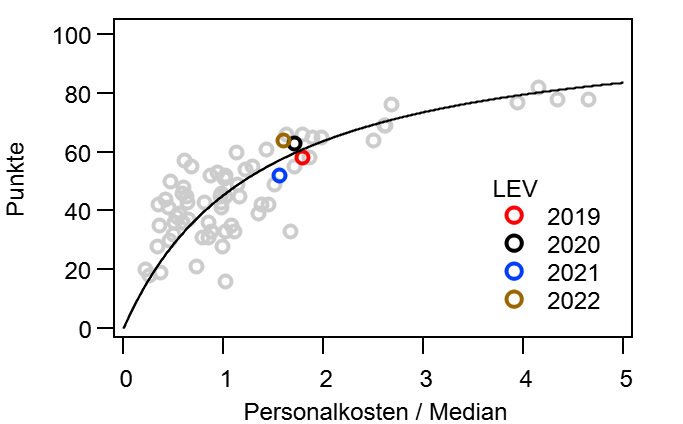
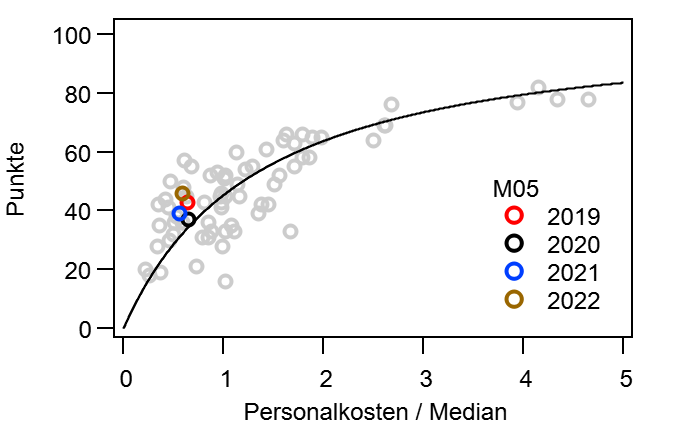
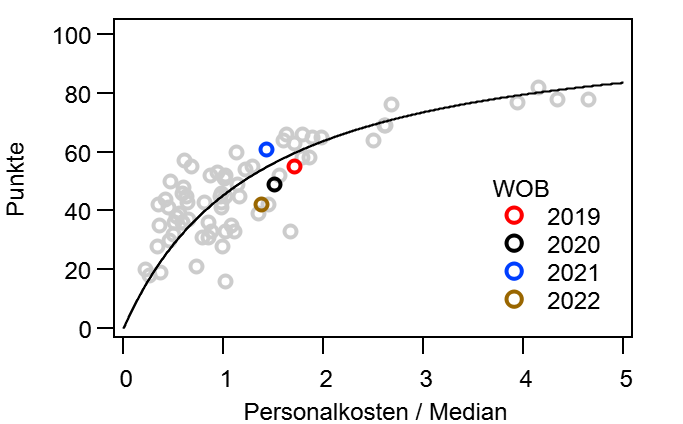
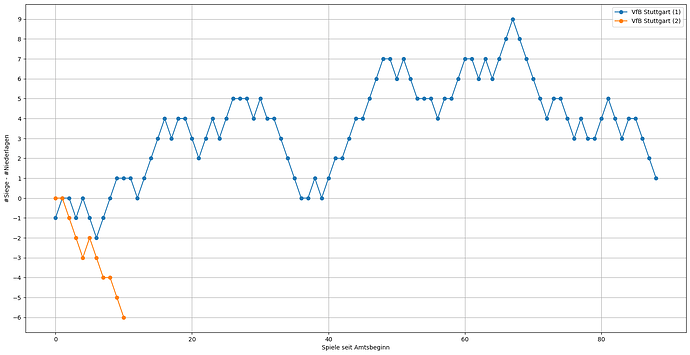
Wenn man sich jetzt aber mal die Endtabelle anschaut, stellt man fest: Die entspricht ja gar nicht dem Power Ranking! Bei Z=20 ist der Zufall so groß, dass er sich über eine Saison nicht wegmitteln kann. In Abbildung 3 sind nun drei Saisonverläufe dargestellt: Die echten Daten (Kreise) und zwei simulierte Saisonverläufe mit Z=20, einmal mit der Endtabelle as Referenz (schwarz) und einmal mit dem tatsächlichen Power Ranking (orange). Wenn ich die Endtabelle als Referenz nehme, wird der Saison natürlich bei 0% enden, da die Tabelle am letzten Spieltag mit sich selbst verglichen wird. Beim Vergleich mit dem tatsächlichen Power Ranking ergibt sich dagegen der eingangs erwartete asymptotische Verlauf, der nach 34 Spieltagen jedoch bei Weitem noch nicht nahe der 0% ist. Wenn man diesem simplen Modell halbwegs Glauben schenken möchte, besteht die Tabelle nach einer Saison je nach Zählweise noch zu etwa 40% aus Unordnung! Oder anders Ausgedrückt: Eigentlich ist die Bundesliga Saison (nach diesem Modell) viel zu kurz.
Abbildung 3
(An dieser Stelle noch der Hinweis: Ich möchte nicht den Bayern ihre Meisterschaft absprechen. Die haben diese absolut verdient gewonnen (was ja irgendwie das Problem der BuLi ist). Es geht hier um Teams die nahe beieinander liegen, also zum Beispiel beim Kampf um die internationalen Plätze, wo wenige Punkte und Tore den Unterschied machen.)
Sagen sie „Stopp“
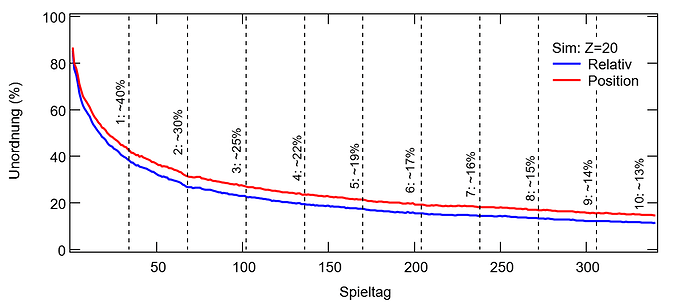
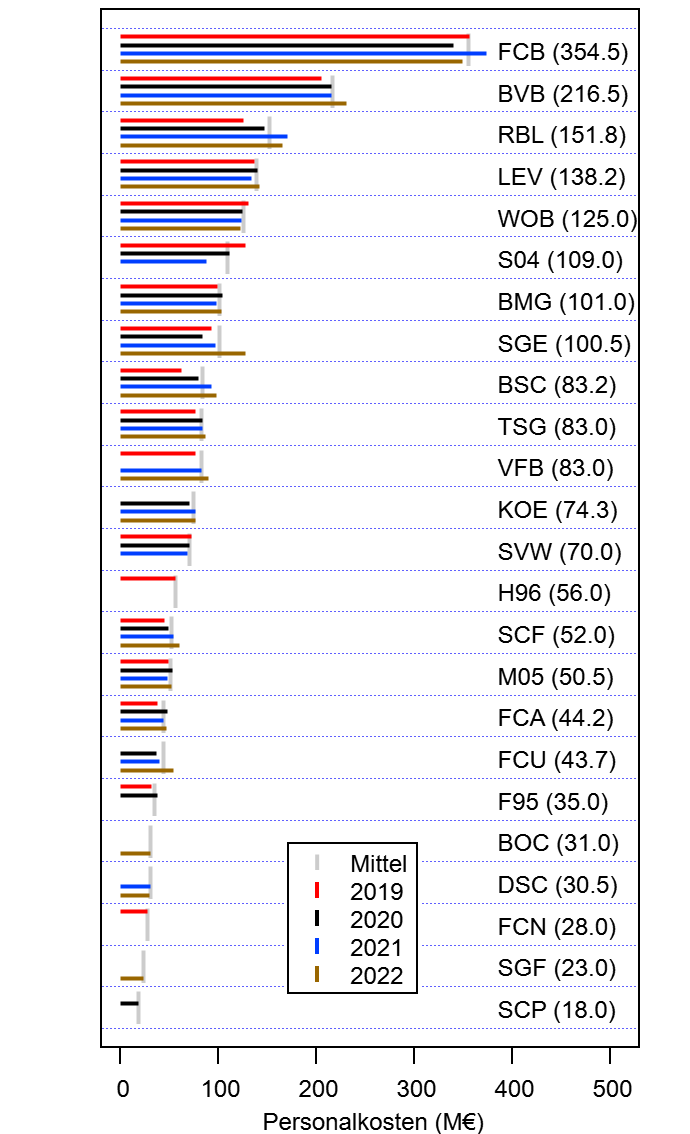
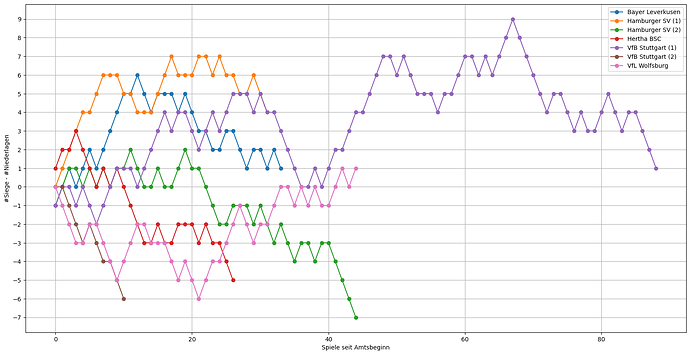
Wie lang müsste die Saison denn dann eigentlich sein? In Abbildung 4 ist der mittlere Saisonverlauf dargestellt (Power Ranking als Referenz), wenn eine Saison 10 Jahre gehen würde. Dafür habe ich nicht die gleiche Saison 10 mal spielen lassen sondern verschiedene Spielpläne gemischt um irgendwelche Artefakte zu vermeiden. Wie oben erwähnt, ist nach einem Jahr noch etwa ein 40% Unordnung in der Tabelle, während es nach 3 Jahren noch ein Viertel sind. Um den Wert auf 10% zu drücken muss man schon mehr als 10 Jahre spielen lassen. Um das ganze etwas Anschaulich zu gestalten: Nach 2 Jahren sind die Teams im Mittel noch knappe zwei Plätze von ihrem tatsächlichen Power Ranking entfernt und nach 8 Jahren noch ein Platz im Mittel.
Abbildung 4
Hier muss aber ein sehr großes Sternchen gemacht werden, da wir schon jenseits der Grenzen dieses einfachen Modells sind. Um den tatsächlichen mittleren Verlauf zu reproduzieren haben wir ein fixes/statisches Power Ranking definiert und dann ausreichend „Zufall“ hinzugefügt, der alle möglichen Faktoren erschlägt. In der echten Welt gibt es neben dem Zufall viele weitere Faktoren wie Verletzungen, Transfers, Trainerwechsel, Dreifachbelastung, Form und so weiter und so fort. Das heißt in der Realität ist das Power Ranking eben nicht statisch sondern verändert sich ständig. Dementsprechend würde eine Saison über 10 Jahre vermutlich gar nicht konvergieren, also sich nicht asymptotisch einen festen Wert nähern. Für eine einzelne Saison sollte das Modell aber eine halbwegs passable Näherung sein um das den Zufall – bzw das „Unerwartete“ – messbar zu machen.
Wenn man hier einen anschaulicheren Vergleich bemühen möchte: Eine Saison der Bundesliga ist wir ein unterbelichtetes Foto, bei dem die Anzahl der Spieltage der Belichtungszeit entspricht. In meinem simplen Modell war das Motiv aber ein einfaches Stillleben. Das heißt man könnte einfach die Belichtungszeit erhöhen und irgendwann wird man jedes Details genau erkennen können. In der echten Welt bewegt sich das Motiv aber. Eine längere Belichtungszeit wäre zwar heller, aber das eigentlich Motiv wäre verwaschen. Für kurze Belichtungszeiten sind die beiden Bilder aber vergleichbar.
Warum aber macht man es nicht einfach „heller“? Das liegt an der Natur des Fußballs. Der ist nämlich deswegen so „dunkel“, weil so wenig Tore fallen. Hätten wir Ergebnisse wie beim Basketball, gäbe es deutlich weniger „glückliche“ Siege, da man schwerer ein 1:0 nach Hause mauern kann. Auch Fehlentscheidung des Schiris wären dann nicht ganz so gewichtig. Dadurch hat dort meiner Meinung nach jedes einzelne Spiel mehr Aussagekraft als beim Fußball. Die entscheidende Frage wäre aber: Wollen wir das überhaupt?
Was haben wir heute gelernt?
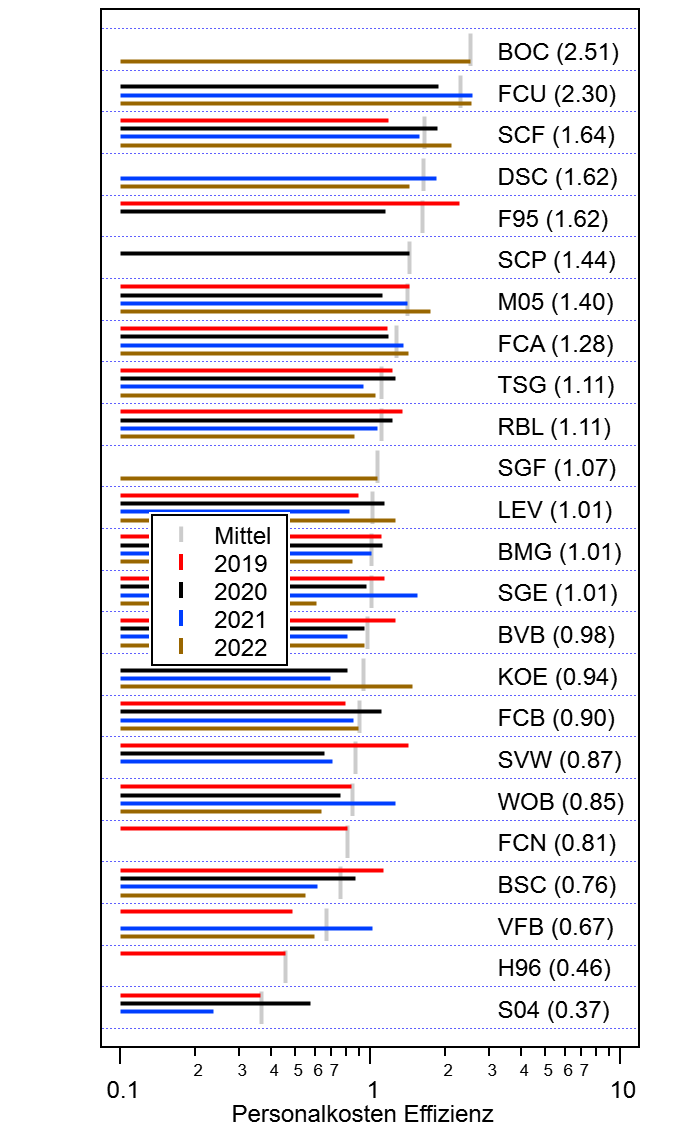
Die Endtabelle der Bundesliga reflektiert nicht unbedingt wie gut ein Team die letzte Saison war, sondern (nur) wie gut es die letzte Saison gespielt hat (duh!). Dabei ist die Endtabelle zu etwa 40% aus „zufälligen“/unvorhersehbaren Faktoren bestimmt. Übrigens hatten @GNetzer und @Taktikfuchs bei ihren Tabellentipps letzte Saison das äquivalent von 42% Unordnung (Relativ Methode), sie waren also ziemlich dicht am vorhersagbaren Möglichen. Respekt!
Das Fazit ist also, wenn man den Vergleich von oben wieder bemühen möchte: Fußball ist wie eine Nacht in der Kneipe oder dem Club; es ist relativ dunkel und etwas chaotisch, aber wir haben unseren Spaß dabei – und ganz genau will man die Details ja gar nicht sehen, denn so bleibt noch Raum für Fantasie, Überraschungen und Hoffnung.
Eine exponentielle Dekorrelation ist schon zu erwarten oder?
Bin mir gerade nicht sicher was genau du damit meinst. Meinst du den konvergenten Verlauf in Abbildung 4? Intuitiv hätte ich da auch auf einen exponentielles Abfallen erwartet, aber so wirklich passt so ein Verlauf nicht. Es lässt sich aber erstaunlich gut mit einem 1/wurzel(x) Verlauf annähern. Habe da auch kein genaues Modell zu aber es könnte vermutlich auch einfache Fehlerrechnung und Annäherung an den Mittelwert sein.
Ja ganz genau ist es nicht. Aber man könnte mal so ein paar 1000 Saisons simulieren, und dann schauen.
Gibt es eigentlich öffentlich zugängliche „echte“ Datenbanken mit aktuellen Statistiken von (mindestens) Bundesliga-Spielen, die man schnell mal per SQL abfragen kann? Eine JDBC Connection URL würde ja schon reichen.
Auf reddit hat jemand für die fünf Top Ligen Grafiken gepostet mit den Trainern welche die höchste Gewinnwahrscheinlichkeiten seit 2000 haben:
https://www.reddit.com/gallery/1181pkj
Dabei möchte ich den Scheinwerfer gerne auf Italien richten. In den anderen Ligen waren die meisten Trainer bei nur einem Verein, aber in Italien ist nur Garcia auf Platz 10 ein one-club-coach. Woran liegt das? Ist deren Trainerpool kleiner? Ist es dort normaler zum Rivalen zu wechseln? Bzw: Ist es dort üblicher einen erfolgreicheren Trainer wegzukaufen? Eventuell könnte @GNetzer das bei der nächsten Ligatour nachfragen, falls Zeit und Platz ist?
Meine Vermutung wäre, dass in Italien das ligainterne Trainerkarussell einfach stärker ist aus verschiedenen Gründen. Die meisten italienischen Vereine stellen nach wie vor hauptsächlich italienische Trainer an, die dann natürlich schon bei anderen italienischen Vereinen waren. Da unterscheiden sich die Ligen alle etwas.
Bundesliga und Serie A: Auch hier holen gefühlt sehr viele Vereine gerne einheimische Trainer, die schon bei anderen Vereinen waren. Will gar nicht wissen, bei seiner wievielten Bundesligastation ein Bruno Labbadia gerade ist. Natürlich sind in Deutschland immer einige Schweizer und Österreicher dabei, wie in Frankreich oft Schweizer und Belgier dabei sind, die die Sprache halte schon können. Das macht sich aber an der Spitze nicht so bemerkbar, weil Bayern und PSG halt alles gewinnen und sich regelmäßiginternationale Toptrainer holen.
Spanien: Ähnliche Geschichte wie in der Bundesliga, nur dass du mit Barca und Real zwei Vereine oben hast, die sich regelmäßig internationale Toptrainer holen, die aber so eine starke Rivalität haben, dass Trainer selten wechseln. Gleichzeitig sind das auch zwei Vereine, die dazu tendieren, eigene Klubikonen zum Trainer zu machen, die dann vorher gar nicht unbedingt große Erfolge gehabt haben müssen. Außerdem hast du sprachlich den Vorteil, dass südamerikanische Trainer keine neue Sprache lernen müssen.
England: Ausgeglichenere Liga, insofern ähnlicher zu Italien, aber durch den sprachlichen Vorteil (Englisch können halt die meisten) und Liga-Prestige und -Etat kann man sich halt ständig alle möglichen internationalen Toptrainer holen. In der Premier League sind aktuell nur 4 englische Trainer aktiv, verglichen mit 12 deutschen in der Bundesliga, 14 spanischen in La Liga, 14 französischen in Ligue 1 und 16 italienischen in der Serie A.
Zweimal Methadon für die Länderspielwoche:
Zum einen hier ein kurzes Interview mit einem Mathematiker bei 11Freunde, bei dem sie über die letzte WM und Zufall im Fußball reden (eventuell bald hinter paywall?)
Zum anderen eine amüsante Korrelation zwischen den beiden bisherigen Amtszeiten von Terzic:
Anscheinend kann man Beiträge nicht unbregrenzt lang bearbeiten, daher die neuste Version der BuLi Ergebnisse hier:
Letztes Update: Nach dem 25. Spieltag, Saison 2022/23
BuLiMatches.zip (131,6 KB)
Sehr interessant.
Das würde ich gern mal für Labbadia beim VfB sehen.
Fragestellung: Wie gut gehen die Bundesligateams diese Saison mit Rückständen (oder Führung) um?
Falls euch die absoluten Zahlen interessieren, hilft Transfermarkt für beides weiter (Rückstand, Führung). Das sind wie gesagt absolute Zahlen, aber um sie vergleichbar zu machen, muss man diese vorher zweimal „renormieren“:
Das gleiche kann natürlich auch für dem Verhalten nach Führung gemacht werden, wobei der entscheidende Wert nicht „Punkte“ sondern „Punktverlust“ ist:
Quelle waren die oben verlinkten Transfermarkt Seiten und Stichtag war nach dem 26. Spieltag.
Wie viele ja wissen wurden vor Kurzem die Kennzahlen der DFL Mitglieder veröffentlicht, inkl. den Personalkosten. Wenn ich Max richtig verstanden hatte ist dies ein guter Messwert wieviel Geld ein Verein in seinen Kader investiert und damit auch wie gut er sein sollte. Hier ein kleine Übersicht der Personalkosten aller Bundesligisten seit der Saison 2018/19:
Einfach Zahlen darstellen ist aber langweilig, daher hatte ich mir die Frage gestellt: Wie gut/effizient sind die Vereine eigentlich mit dem Geld, welches sie in den Kader investieren? Dafür habe ich mit vereinfachten Annahmen ein simples Model zusammen geklöppelt, welches für die Interessierten etwas genauer hier erklärt wird:
Wie immer müssen solche Werte wie die Personalkosten zunächst renormiert werden, wobei hier der Median die bessere Referenz dafür ist, also das arithmetische Mittel (aka Durchschnitt). Der Median ist weniger anfällig, wenn ein paar wenige Clubs sehr viel mehr Geld haben und für einen kleinen Verein spielt es für die Punkte am Ende keine Rolle ob er mit 0:3 oder 0:9 verliert.
Als nächstes ist die Annahme, dass die renormierten Personalkosten (K) in etwa exponentiell mit der Qualität (Q) steigen. Außerdem soll die Qualität Null sein für K=0, weil ohne Geld gibts keine Spieler. Für diese Randbedingungen bietet sich die folgende Formel an:
Im Umkehrschluss heißt dies, dass die Qualität logarithmisch von den Personalkosten abhängt:
Da die Qualität Q ein relativer Wert ist, können wir sie normieren wie wir wollen und in diesem Fall wählen wir, dass ein mittlmäßiger Verein mit K = 1 auch einen Qualität von Q = 1 hat. Dadurch können wir einen der zwei Parameter loswerden und wählen
und erhalten
Um von der Qualität eines Teams jetzt auf die erwartbaren Punkte P zu kommen, brauchen wir eine Funktion die bei Q = 0 auch Null ergibt (keine Qualität, keine Punkte) und sich asymptotisch dem Maximum von 102 Punkten nähert, wenn Q immer größer wird. Der einfachste Ansatz ist wieder eine exponentielle Funktion
Hier können wir wieder eine Annahme treffen um einen Parameter loszuwerden: Ein mittelmäßiges Team (Q = 1) sollte in etwas gleich viele Siege wie Niederlagen wie Unentschieden haben, also 45.33 Punkte in der Saison. Damit können wir c bestimmen mit:
und erhalten
Wenn wir jetzt noch für Q die Formel in Abhängigkeit der Personalkosten K einsetzen erhalten wir:
Es bleibt also nurnoch der Parameter A über, der bestimmt wie extrem die Preise mit der Qualität des Kaders wachsen. Beim Fitten (Minimierung der quadratischen Abweichung in x-Richtung) ergab sich ein Wert von A = 1.58. Andere Fitting Methoden ergaben andere Resultate – je nachdem was man priorisiert – aber dieser Wert passte am besten zu den reicheren Clubs. Es gibt auch eine Begründung warum es Sinn ergibt, sich eher an denen zu orientieren als an den „sub-median“ Vereinen, siehe unten.
Schnell zusammengefasst war die erste Annahme, dass der Median der Personalkosten in der BuLi der beste Referenzwert ist und alle Vereine darauf normiert wurden (Personalkosten geteilt durch Median der Saison). Danach gehen wir davon aus, dass die Personalkosten mit der Kaderqualität (grob) exponentiell anwachsen und sich die erwartete Punktzahl eines Vereines stetig dem maximalen Wert von 102 Punkten annähern – mit steigender Kaderqualität. Bei dem Modell verblieb am Ende ein Parameter, der besagte wie stark die Kosten exponentiell mit der Qualität steigern. Wenn man den Wert dann an die bestehenden Daten anfittet, erhalten wir die folgende Kurve:
Es ist zunächst auffällig, dass Bayern und Dortmund (die beiden Inseln um 2.8 und hinter 4) ziemlich genau auf dem Fit liegen. Dies liegt daran, dass die beiden natürlich den Fit dahinten dominieren und im gewissen Sinne die Referenz vorgeben.
Auf den Daten basierend können wir aber nun anschauen wie gut die einzelnen Vereine für ihre Personalkosten so abgeschnitten haben. Dafür nehmen wir die Punkte die ein Verein erzielt hat und vergleichen mittels des Models welche erwarteten Personalkosten der Verein dafür hätte aufbringen sollen. Wenn wir dann die tatsächlichen Personalkosten durch den erwarteten Wert teilen, sehen wir wie effizient die Vereine ihr Geld ausgeben. Erhalten wir einen Wert von 1, hieße das der Verein verhält sich absolut im erwartbaren Soll. Hat ein Verein einen Wert von 2 könnte man sagen, der Verein setzt jeden Euro so gut ein, dass er effektiv wie zwei Euro wirkt. Ein Wert von unter 0,5 wäre dementsprechend das Gegenteil und der Verein ist nur halb zu effizient wie er sein sollte. Für alle Bundelsiga Vereine seit der Saison 2018/19 sieht das dann wie folgt aus:
Glückwunsch an Bochum, die hier den ersten Platz abräumen. Generell fällt es auf, dass vorallem die „kleinen“ Clubs ganz oben auftauchen. Anfangs dachte ich, dass mein kleines Model komplett falsch ist, aber ich denke dies ist ein Fall von Survivorship Bias: „Kleine“ Vereine kommen überhaupt nur in die Bundesliga (und halten sich da dann auch), wenn sie überdurchschnittlich gute Arbeit leisten. Schlecht wirtschaftende Vereine mit geringem Budget werden vorher schon aussortiert – aka sind einfach nicht im Oberhaus zu finden.
Kleine Dinge die mir gerade auffallen:
Weitere Dinge die euch auffallen, könnt ihr sehr gerne hier teilen 
Und falls ihr wissen wollt wo euer Verein im zweiten Graphen ist, hier noch einmal für alle Vereine zum nachgucken:
Hier noch einmal die aktuelle csv-Datei mit allen Bundesliga Ergebnissen:
Letztes Update: Nach dem 34. Spieltag, Saison 2022/23
BuLi_Matches.zip (131,6 KB)
Nachträglich ist mir gerade noch aufgefallen, wie dicht Gladbach sich an der Kurve entlang bewegt. Ein echter „Modellverein“ 
Late to the party, aber ich hab mir mal den Spaß gegönnt 
Hier die Verlaufskurve für beide Amtszeiten beim VfB:
Hier ist der (etwas konfuse) Plot für sämtliche Vereine:
Und hier nochmal die VfB-Zeit, aber mit einer Verlaufskurve für die Tordifferenz:
Hier auch der Code (Python / Jupyter Notebook), falls jemand noch selber damit rumspielen will:
code.zip (305,2 KB)
Ich hätte mal eine (Um-)frage an Leute die sich damit eventuell etwas auskennen oder einfach eine Denksportaufgabe hätten:
Angenommen ihr dürft euch nur zwei statistische Werte [1] einer Mannschaft anschauen um dadurch eine möglichst gute Idee zu haben wie diese Spielt: Welche zwei Werte würdet ihr nehmen?
Beispiel: „Ballbesitzanteil“ und „Progressiv Passing Distance / Total Passing Distance“. Der Ballbesitztanteil könnte ein Hinweis sein ob eine Mannschaft eher tief steht und abwartet oder hoch presst um schnell den Ball wieder zu haben. Das Verhältnis zwischen Progressive Passing Distance und Total Passing Distance wäre dann ein Zeichen was die Mannschaft dann mit dem Ball macht: Viel hinten rum oder direkt steil nach vorne?
Natürlich bekommt man nicht alle Feinheiten abgedeckt (ein Dribbling wäre komplett raus in dem Beispiel), aber das liegt dann halt in der Natur der Sache wenn man es auf zwei Werte kondensiert. Um so mehr würde mich daher interessieren welche Werte-Paare euch da so in den Sinn kommen würden.
[1]: ermittelt durch Werte die man auf FBref.com findet. Ein Beispiel wäre hier wobei ihr unter „2022-2023 Match Log Types“ verschiedene Aspekte des Spiels auswählen könnt und im „Glossary“ stehen dann alle statistischen Werte mit Erklärung.
